Units and measurements are an important scientific and mathematical concept, which is useful in every field. The study of units and measurements is not only important in science, mathematics, and engineering, but it also makes important contributions to physics, chemistry, and other fields. A good understanding of units and measurements can help us in the natural division of the world, its research, and scientific study. Therefore, it is an important topic that every student should understand.
units and measurements
To calculate physical quantities like time, mass and length, we need some standards of measurement. These standards of measurement are called units of physical quantities. In this article, we will provide detailed information about units and measurements.
Why do we need standard units and measurements?
There are many methods and units to calculate various quantities like area, mass, length, volume, etc. For example,
- An acre is a traditional way of measuring size in India. According to the metric system, one acre is equal to 4046 square meters.
- Temperature is calculated in degrees Celsius, but the length of a rod cannot be measured in the same unit.
So, it can now be estimated how difficult it would be to measure quantities without standard terms. Each zodiac sign should be measured in its own way. The magnitude and measurement vary along with the amount. Therefore the need for units of measurement arises for every quantity.
Basic physical quantities/units
Those quantities which can describe the laws of physics are called physical quantities. A physical quantity is one that can be measured. Thus, length, mass, time, pressure, temperature, current and resistance are considered physical quantities. The units of quantities are called basic units. Physical quantities are classified into two parts
basic amounts or base amounts
Those physical quantities which are independent from each other are called fundamental quantities.
| Basic quantities and units | |||
| Amount | unit | Sign | Definition |
| Length | meter | m | One meter is the distance traveled by light in a vacuum during a time interval of (1/299792458) seconds. |
| Mass | Kilogram | kg | This is the mass of a platinum-iridium cylinder kept in the National Bureau of Weights and Measures in Paris. |
| Time | seconds | s | Second is the time taken by light of a specified wavelength emitted by a cesium-133 atom to vibrate 9192631770. |
| Electric current | ampere | A | An ampere is the current which, when flowing through two straight parallel conductors of infinite length and negligible cross-sectional area, placed 1 meter apart in vacuum, produces between them a force equal to 2 x 10-7 newtons per meter of length. Generates. |
| temperature | kelvin | K | It is 1/273.6 of the thermodynamic temperature of the triple point of water. |
| amount of substance | value | mol | One mole is the amount of substance that contains elementary units equal to the number of atoms in 0.012 kg of carbon-12. |
| light intensity | cadella | cd | One candela is defined as 1/60th of the luminous intensity of 1 square centimeter of an ideal black body kept at the freezing temperature of platinum (1773 0C). |
Apart from these seven zodiac signs, there are also two supplementary zodiac signs.
| Complementary quantities and units | |||
| Amount | unit | Sign | Definition |
| flat angle | radian | rad | Radian is the angle subtended by an arc at the center of the circle whose length is equal to the radius of the circle. |
| solid angle | steradian | sr | Steradian is the solid angle subtended by a spherical surface at the center of a sphere of area equal to the square of its radius. |
derivative amounts
All other quantities which can be expressed in terms of fundamental quantities are called derived quantities.
| Derived quantities and units | |
| Amount | unit |
| displacement | m |
| Area | m2 |
| volume | m3 |
| velocity | ms-1 |
| acceleration | ms-2 |
| density | Kg m-3 |
| Impulse | Kg ms-1 |
| work/energy/heat | Joule (or) Kg m2/sec2 |
| Power | Watt(W) (or) Joule/sec |
| angular velocity | rad s-1 |
| angular acceleration | rad s-2 |
| moment of inertia | Kg m2 |
| Force | Newton (or) Kg m/sec2 |
| pressure | Newton/m (or) Kg m-1/sec2 |
| impulse | Newton sec (or) Kg m/sec |
| inertia | Kg m2 |
| Electric current | ampere (or) C/sec |
| resistance/impedance | Ohm (or) Kg m2/sec C2 |
| EMF/Voltage/Potential | Volt (or) Kg m2/sec2 C |
| magnetism | Henry/m (or) Kg m/C2 |
| electrical conductivity | Faraday/m (or) sec2C2/Kgm3 |
| frequency | hertz (or) sec-1 |
| wavelength | m |
system of units
- FPS Method: In this system the unit of length is foot, the unit of mass is pound and the unit of time is second.
- CGS Method: In this system the units of length, mass and time are centimeter, gram and second respectively.
- MKS Method: In this system the units of length, mass and time are meter, kilogram and second respectively.
- SI system: This method is widely used in all measurements throughout the world. This system is based on seven basic units and two supplementary units.
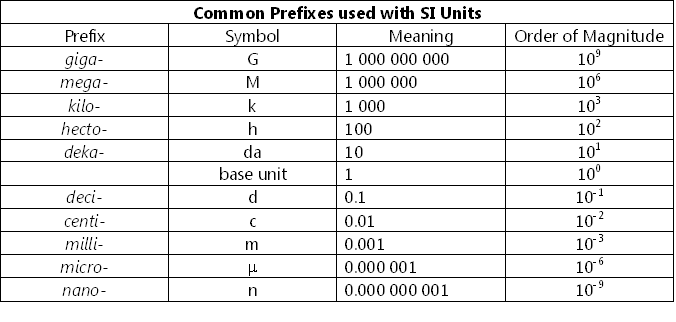
SI unit prefix
The SI system uses a standard system of prefixes for base units, making them more relevant and descriptive in relative magnitude. Prefixes are used to identify multiples or fractions of the base unit. The table below lists the standard prefixes for SI units of measurement.
Dimensions and dimensional formulas
The dimensions of a physical quantity are the powers (or exponents) by which the base quantities are raised to represent that physical quantity. Dimensional equations are those equations which represent the dimensions of a physical quantity as base quantities.
For example,
- Dimensional formula of volume, (V) = (M0L1T-1,
- Dimensional formula of speed, (v) = (M0LT-1,
- Dimensional formula of force, (F) = (M1L1T-2,
- Mass density, (ρ) = (ML3T0,
How is a dimensional formula written for a physical quantity?
- The formula for physical quantity must be written. The quantity should be on the left side of the equation.
- All quantities on the right-hand side of the formula should be written as fundamental quantities such as mass, length, and time.
- Replace mass, length and time with M, L and T respectively.
- Write the powers of the terms.
- According to the principle of homogeneity of dimensions, all terms in a given physical equation must be equal.
For example, s = ut + (½) at2
Equation according to dimensions, (L) = (LT-1.T) + (LT-2, T2) (L) = (L) + (L) Left side = Right side
Features of dimensions
- Dimensions do not depend on the system of units.
- Quantities with the same dimensions can be added or subtracted from each other.
- Dimensions can be derived from units of physical quantities and vice versa.
- Two different quantities can have the same dimensions.
- When two dimensions are multiplied or divided, it will form a third dimension.
Units and dimensions of some derived quantities
| Derived quantities and dimensions | |
| Amount | dimensional formula |
| displacement | M0L1T0 |
| Area | M0L2T0 |
| volume | M0L3T0 |
| velocity | M0L1T-1 |
| acceleration | M0L1T-2 |
| density | M1L-3T0 |
| Impulse | M1L1T-1 |
| work/energy/heat | M1L2T-2 |
| Power | M1L2T-3 |
| angular velocity | M0L0T-1 |
| angular acceleration | M0L0T-2 |
| moment of inertia | M1L2T0 |
| Force | M1L1T-2 |
| pressure | M1L-1T-2 |
| impulse | M1L1T-1 |
| inertia | M1L2T0 |
| Electric current | Q.T.-1 |
| resistance/impedance | ML2T-1Q-2 |
| EMF/Voltage/Potential | ML2T-2Q-1 |
| magnetism | MLQ-2 |
| electrical conductivity | T2Q2M-1L-3 |
| frequency | T-1 |
| wavelength | L1 |
Applications of Dimensional Analysis
- To check the correctness of a physical equation.
- To obtain relations between various physical quantities.
- Converting a physical quantity from one system of units to another.
Sharing is caring!
